МЕХАНИКА И МАШИНОСТРОЕНИЕ – Численные вычисления и анализ данных
Механика и машиностроение — Численные расчеты и анализ данных. Научная конференция 2019, 19–21 апреля 2019 г., Пекин
19-21 апреля 2019 г., Пекин, Китай
Исследование поведения слоистого расширения современных композитных ламинатов, армированных углеродным волокном
Гонг Ю1*, Ван Яна2, Пэн Лэй3, Чжао Либинь4, Чжан Цзяньюй1
1Чунцинский университет, Чунцин, 400044, Китай
2Китайский авиационный научно-исследовательский институт, Пекинский научно-исследовательский институт авиационных материалов, Пекин, 100095, Китай
3Китайская коммерческая авиация Пекинский центр исследований и разработок в области гражданской авиации, Пекин, 102211, Китай
4Пекинский университет аэронавтики и астронавтики, Пекин, 100191, Китай
АбстрактныйСлоистая структура – одна из наиболее распространённых конфигураций композитных материалов, но расслоение становится основным видом разрушения из-за слабых межслойных свойств. Исследования расслоения и расширения многослойных ламинатов, широко используемых в инженерной практике, всегда были актуальной темой для учёных. В данной статье представлены результаты исследований расслоения композитов, армированных углеродным волокном, в Чунцинском университете и Лаборатории усталостного разрушения Пекинского университета аэронавтики и астронавтики с точки зрения экспериментальных исследований и численного моделирования. В заключение, рассматривается перспективное направление развития данной области.
Ключевые слова:композит, армированный углеродным волокном, ламинат, расслоение, усталостное расслоение
введение
Композитные материалы обладают превосходными свойствами, такими как высокая удельная прочность и высокая удельная жёсткость, и широко используются в аэрокосмической промышленности, энергетике, гражданском транспорте и строительстве. В процессе обработки и эксплуатации композитных материалов волокна и матрица подвергаются различным повреждениям под нагрузкой. К распространённым видам разрушения композитных ламинатов относятся межслоевые и внутрислоевые повреждения. Из-за отсутствия армирования по толщине латеральные механические свойства ламината неудовлетворительны, и при внешних ударных нагрузках высока вероятность расслоения. Возникновение и расширение стратифицированных повреждений приведёт к снижению жёсткости и прочности конструкции и даже к катастрофическим авариям.[1-3]Таким образом, проблема расслоения все больше и больше затрагивается при проектировании конструкций и анализе прочности композитных материалов, и необходимо изучать поведение композитных материалов при послойном расширении.[4].
Исследование поведения ламината при послойном расширении
1. Экспериментальное исследование
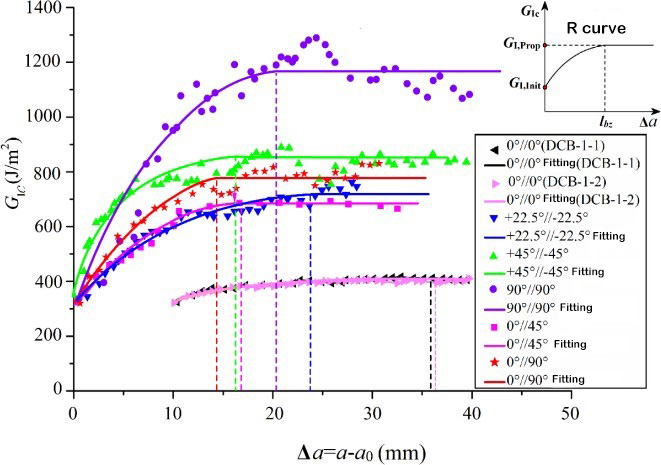
Межслойная вязкость разрушения является характерным параметром механических свойств между слоями композита. Соответствующие стандарты испытаний были установлены для определения межслойной вязкости разрушения гибридных однонаправленных ламинатов типа I, типа II и I/II. Соответствующая испытательная установка показана на рисунке 1. Однако многонаправленные ламинаты композитных материалов часто используются в реальных инженерных конструкциях. Поэтому экспериментальное исследование поведения расслоения и расширения многонаправленных ламинатов имеет более важное теоретическое значение и инженерную ценность. Инициирование и расширение слоев многослойного ламината происходят между интерфейсами с произвольными углами наслаивания, а поведение послойного расширения существенно отличается от поведения однонаправленных ламинатов, а механизм расширения более сложен. Исследователи имеют относительно мало экспериментальных исследований многонаправленных ламинатов, и определение межслойной вязкости разрушения еще не установило международный стандарт. Исследовательская группа использовала углеродное волокно T700 и T800 для разработки различных композитных ламинатов с различными углами наложения слоев на границе раздела и изучала влияние угла наложения слоев на границе раздела и перемычек волокон на статическое и усталостное расслоение. Было обнаружено, что перемычки волокон, образуемые задней кромкой слоя, оказывают большое влияние на межслойную вязкость разрушения. По мере расширения слоя напластования межслойная вязкость разрушения постепенно увеличивается от более низкого начального значения, и когда слой напластования достигает определенной длины, она достигает стабильного значения, то есть эффекта кривой сопротивления R. Начальная вязкость разрушения межслоя практически равна и приблизительно равна вязкости разрушения смолы, которая зависит от вязкости разрушения самой матрицы.[5, 6]Однако значения межслойной вязкости разрушения при растяжении различных интерфейсов значительно различаются. Представлена значительная зависимость угла между слоями интерфейса. В ответ на эту зависимость Чжао и др.[5]Основываясь на физическом механизме источника расслоенного сопротивления, считается, что значение стабильности вязкости разрушения межслойного слоя состоит из двух частей: одна часть - это работа разрушения интерфейса несвязанных слоев, а другая часть - это внутрислоевое повреждение и волокно. Работа разрушения, вызванная перемычками. С помощью конечно-элементного анализа поля фронта напряжений слоистого фронта обнаружено, что вторая часть работы разрушения зависит от глубины зоны повреждения фронта расслоения (как показано на рисунке 3), а глубина зоны повреждения пропорциональна углу наложения интерфейса. Представлена теоретическая модель значения стабильности вязкости разрушения I-типа, выраженная синусоидальной функцией угла интерфейса слоя.
Гонг и др.[7]Проведено испытание гибридного расслоения I/II при различных соотношениях компонентов смеси и установлено, что гибридное расслоение I/II в ламинате также имеет существенные характеристики кривой сопротивления R. Анализ вязкости разрушения между различными образцами показал, что начальное и стабильное значения межслойной вязкости разрушения образца значительно увеличиваются с увеличением соотношения компонентов смеси. Кроме того, начальная и стабильная вязкости разрушения межслоевого слоя при различных соотношениях компонентов смеси может быть описана критерием BK.
Что касается усталостного расслоения, то в ходе испытания также наблюдалось значительное перекрытие волокон. Анализ данных испытаний показал, что расширение композитного материала при усталостном расслоении зависит от «кривой сопротивления», поэтому традиционная модель скорости расширения усталостного расслоения и пороговое значение больше не применимы. На основе теоретического анализа Чжан и Пэн[4,8,9]Ввели понятие сопротивления усталостному расслоению для выражения энергии, необходимой для усталостного расслоения композитных материалов, и далее предложили нормализованную энергию деформации. Скорость высвобождения представляет собой модель скорости стратифицированного усталостного расширения и пороговое значение управляющих параметров. Применимость модели и нормализованного порогового параметра подтверждена экспериментально. Далее, Чжао и др.[3]Всесторонне рассмотрели влияние перекрытия волокон, соотношения напряжений и соотношения смешивания нагрузки на усталостное расслоение и поведение расширения, а также разработали нормализованную модель скорости расширения стратифицированного усталостного расширения, учитывающую влияние соотношения напряжений. Точность модели была подтверждена испытаниями на усталостное расслоение с различными соотношениями напряжений и соотношениями смешивания. Что касается физической величины сопротивления расширению стратифицированного усталостного расширения в модели нормализованной скорости расширения стратифицированного усталостного расширения, Гонг и др.[1]Преодолеть недостаток метода расчета, позволяющего получать лишь ограниченные дискретные данные экспериментально, и определить усталость с точки зрения энергии. Разработана аналитическая модель для расчета сопротивления расслоенному растяжению. Модель позволяет количественно определить усталостное расслоение и сопротивление расширению, а также предоставить теоретическую поддержку для применения предлагаемой модели нормализованной скорости усталостного расслоения.
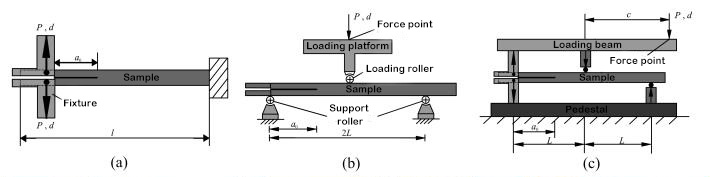Рисунок 1. Схема стратифицированного испытательного устройства
Рисунок 2 Кривая сопротивления межслойной трещиностойкости R[5]
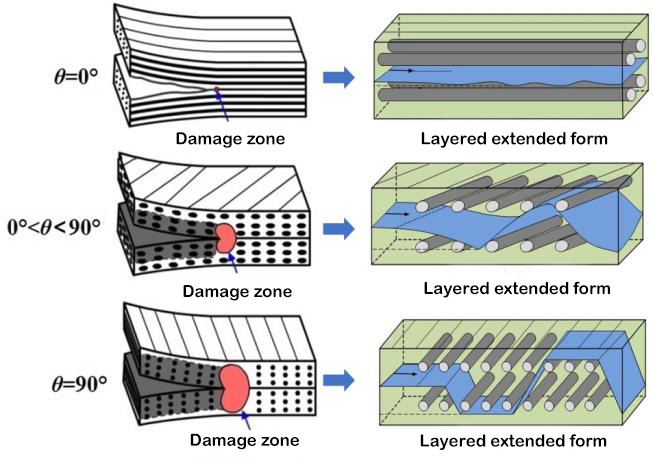
Рисунок 3. Зона повреждения слоистой передней кромки и слоистая протяженная морфология[5]
2. Численное моделирование
Численное моделирование расширения слоев является важным направлением исследований в области проектирования композитных конструкций. При прогнозировании расслоения композитных однонаправленных ламинатов существующие критерии расширения слоев обычно используют постоянную межслойную вязкость разрушения в качестве основного эксплуатационного параметра.[10], сравнивая скорость высвобождения энергии в вершине трещины и межслойную вязкость разрушения. Размер для определения расширения слоев. Механизм разрушения многонаправленных ламинатов сложен.[11,12], который характеризуется значительными кривыми сопротивления R[5,13]Существующие критерии послойного расширения не учитывают эту особенность и не применимы к моделированию расслоения волокнистых мостиковых разнонаправленных ламинатов. Гонг и др.[10, 13]Улучшены существующие критерии стратифицированного расширения и предложено ввести в них кривую сопротивления R, на основе чего разработан критерий стратифицированного расширения, учитывающий влияние перемычек волокон. Определение и параметры использования билинейного составного когезионного блока были систематически изучены численными методами, включая начальную жесткость интерфейса, прочность интерфейса, коэффициент вязкости и минимальное количество элементов в зоне когезионной силы. Была создана соответствующая модель параметров когезионной группы. Наконец, эффективность и применимость улучшенного критерия стратифицированного расширения и модели параметров когезионной группы проверены статическим испытанием на стратификацию. Однако улучшенные критерии могут быть использованы только для одномерного моделирования слоёв из-за позиционных зависимостей, а не для двумерных или трёхмерных иерархических расширений. Для решения этой проблемы автор также предложил новый трилинейный составной когезионный блок, учитывающий перемычки волокон.[14]. Конститутивное соотношение описывает сложный процесс послойного расширения с микроскопической точки зрения и обладает преимуществами простых параметров и ясного физического смысла.
Кроме того, для точного моделирования явления стратифицированной миграции, распространенного в процессе стратификации многонаправленных ламинатов[11,12], Чжао и др.[11,12]Предложена модель управления траекторией трещины, основанная на расширенном методе конечных элементов, имитирующая специальную конструкцию. Иерархическая миграция в тесте на расслоение композита. В то же время предложена модель слоистого расширения для зигзагообразного расширения вдоль интерфейса 90°/90°, которая точно имитирует поведение слоистого расширения интерфейса 90°/90°.
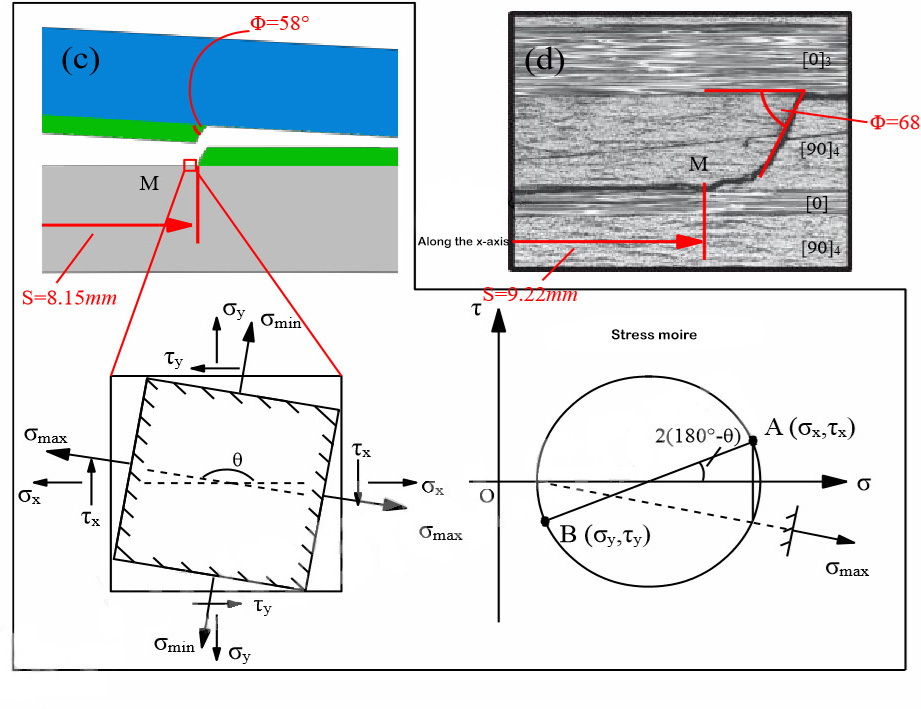Рисунок 4. Численное моделирование слоистой миграции и экспериментальные результаты[15]
Заключение
В данной статье рассматриваются результаты исследований данной группы в области расслоения композитных ламинатов. Экспериментальные аспекты включают в себя, главным образом, влияние угла укладки интерфейса и перемычек волокон на статическое и усталостное расширение при расслоении. Благодаря большому количеству экспериментальных исследований было установлено, что механизм многонаправленного разрушения ламината композитных материалов сложен. Перемычки волокон являются распространенным механизмом упрочнения многонаправленных ламинатов, что является основной причиной кривой сопротивления R при межслойной вязкости разрушения. В настоящее время исследования кривой сопротивления R при расслоении II относительно недостаточны и требуют дальнейших исследований. Исходя из механизма разрушения, предлагается модель усталостного расслоения, включающая различные влияющие факторы, что является одним из направлений исследований усталостного расслоения. С точки зрения численного моделирования исследовательская группа предложила усовершенствованный иерархический критерий расширения и когезионную конститутивную модель для учета влияния перемычек волокон на поведение расслоенного расширения. Кроме того, для более точного моделирования явления иерархической миграции используется расширенный конечный элемент. Этот метод устраняет необходимость в мелком делении ячеек, устраняя проблемы, связанные с переделением сетки. Он обладает уникальными преимуществами при моделировании стратификации произвольных форм, и в будущем необходимы дополнительные исследования его инженерного применения.[16].
Ссылки
[1] Y Gong, L Zhao, J Zhang, N Hu. Новая модель для определения сопротивления усталостному расслоению в композитных слоистых материалах с точки зрения энергии. Compos Sci Technol 2018; 167: 489-96.
[2] L Zhao, Y Wang, J Zhang, Y Gong, N Hu, N Li. Модель на основе XFEM для моделирования роста зигзагообразного расслоения в слоистых композитах при нагрузке в режиме I. Compos Struct 2017; 160: 1155-62.
[3] L Zhao, Y Gong, J Zhang, Y Wang, Z Lu, L Peng, N Hu. Новая интерпретация поведения роста усталостного расслоения в многонаправленных ламинатах из углеродного волокна. Compos Sci Technol 2016; 133: 79-88.
[4] L Peng, J Zhang, L Zhao, R Bao, H Yang, B Fei. Рост расслоения в режиме I многонаправленных композитных ламинатов под усталостной нагрузкой. J Compos Mater 2011; 45: 1077-90.
[5] L Zhao, Y Wang, J Zhang, Y Gong, Z Lu, N Hu, J Xu. Модель платообразной вязкости разрушения, зависящая от интерфейса, в многонаправленных ламинатах из углепластика при нагружении в режиме I. Композиты. Часть B: Инжиниринг. 2017; 131: 196-208.
[6] Чжао Л., Гун И., Чжан Д., Чен И., Фэй Б. Моделирование роста расслоения в многонаправленных ламинатах при нагружении в режиме I и смешанном режиме I/II с использованием связующих элементов. Compos Struct 2014; 116: 509-22.
[7] Y Gong, B Zhang, L Zhao, J Zhang, N Hu, C Zhang. Поведение R-кривой расслоения смешанного режима I/II в углеродных/эпоксидных ламинатах с однонаправленными и многонаправленными интерфейсами. Compos Struct 2019. (На рассмотрении).
[8] L Peng, J Xu, J Zhang, L Zhao. Смешанный рост расслоения многонаправленных композитных ламинатов под усталостной нагрузкой. Eng Fract Mech 2012; 96: 676-86.
[9] Чжан Дж., Пэн Л., Чжао Л., Фэй Б. Скорости роста усталостного расслоения и пороги композитных ламинатов при смешанном режиме нагружения. Int J Fatigue 2012; 40: 7-15.
[10] Y Gong, L Zhao, J Zhang, Y Wang, N Hu. Критерий распространения расслоения, включающий эффект перекрытия волокон при расслоении смешанного типа I/II в многонаправленных ламинатах из углеродного волокна. Compos Sci Technol 2017; 151: 302-9.
[11] Y Gong, B Zhang, SR Hallett. Миграция расслоения в многонаправленных композитных ламинатах при квазистатическом и усталостном нагружении в режиме I. Compos Struct 2018; 189: 160-76.
[12] Y Gong, B Zhang, S Mukhopadhyay, SR Hallett. Экспериментальное исследование миграции расслоения в многонаправленных ламинатах при статическом и усталостном нагружении в режиме II по сравнению с режимом I. Compos Struct 2018; 201: 683-98.
[13] Y Gong, L Zhao, J Zhang, N Hu. Улучшенный критерий степенного закона для распространения расслоения с учетом эффекта крупномасштабного перекрытия волокон в композитных многонаправленных ламинатах. Compos Struct 2018; 184: 961-8.
[14] Y Gong, Y Hou, L Zhao, W Li, G Yang, J Zhang, N Hu. Новая трёхлинейная модель зоны когезии для роста расслоения в ламинатах DCB с учётом эффекта перекрытия волокон. Compos Struct 2019. (Будет представлена)
[15] L Zhao, J Zhi, J Zhang, Z Liu, N Hu. XFEM-моделирование расслоения в композитных ламинатах. Композиты. Часть A: Прикладная наука и производство. 2016; 80: 61-71.
[16] Чжао Либин, Гун Юй, Чжан Цзяньюй. Исследования свойств слоистого расширения композитных ламинатов, армированных волокнами. Журнал авиационных наук, 2019: 1-28.
Источник:Гун Юй, Ван Яна, Пэн Лэй, Чжао Либинь, Чжан Цзяньюй. Исследование свойств стратифицированного расширения современных композитных ламинатов, армированных углеродным волокном [C]. Механика и машиностроение. Численные вычисления и анализ данных. Научная конференция 2019 года. Китайское общество механиков, Пекинское общество механиков, 2019. с помощью иксюешу
Время публикации: 15 ноября 2019 г.